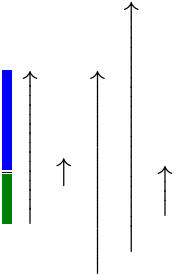
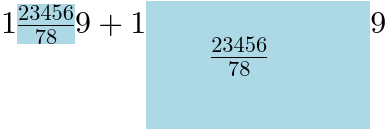
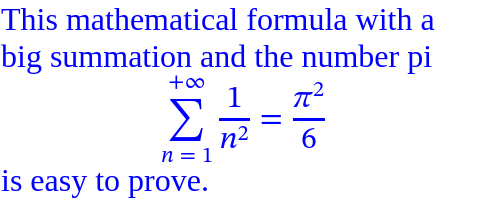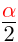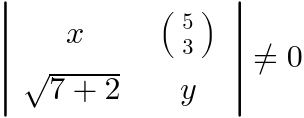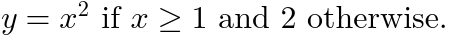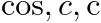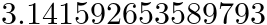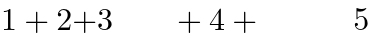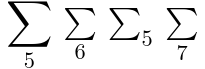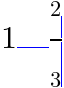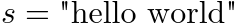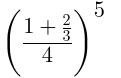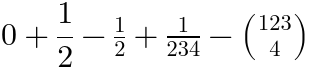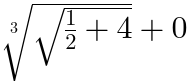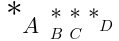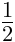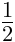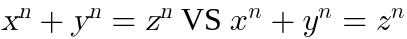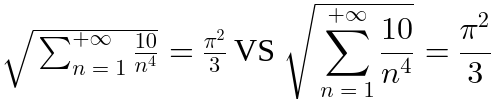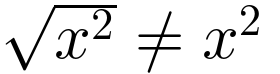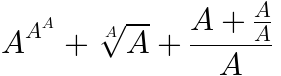| (Content, Form) 键 |
类别 |
313 条(35 个 Unicode 范围)为infix 形式:
[U+2190–U+2195], [U+219A–U+21AE], [U+21B0–U+21B5], {U+21B9}, [U+21BC–U+21D5], [U+21DA–U+21F0], [U+21F3–U+21FF], {U+2794}, {U+2799}, [U+279B–U+27A1], [U+27A5–U+27A6], [U+27A8–U+27AF], {U+27B1}, {U+27B3}, {U+27B5}, {U+27B8}, [U+27BA–U+27BE], [U+27F0–U+27F1], [U+27F4–U+27FF], [U+2900–U+2920], [U+2934–U+2937], [U+2942–U+2975], [U+297C–U+297F], [U+2B04–U+2B07], [U+2B0C–U+2B11], [U+2B30–U+2B3E], [U+2B40–U+2B4C], [U+2B60–U+2B65], [U+2B6A–U+2B6D], [U+2B70–U+2B73], [U+2B7A–U+2B7D], [U+2B80–U+2B87], {U+2B95}, [U+2BA0–U+2BAF], {U+2BB8},
|
A |
108 条(31 个 Unicode 范围)为infix 形式:
{U+002B}, {U+002D}, {U+00B1}, {U+00F7}, {U+0322}, {U+2044}, [U+2212–U+2216], [U+2227–U+222A], {U+2236}, {U+2238}, [U+228C–U+228E], [U+2293–U+2296], {U+2298}, [U+229D–U+229F], [U+22BB–U+22BD], [U+22CE–U+22CF], [U+22D2–U+22D3], [U+2795–U+2797], {U+29B8}, {U+29BC}, [U+29C4–U+29C5], [U+29F5–U+29FB], [U+2A1F–U+2A2E], [U+2A38–U+2A3A], {U+2A3E}, [U+2A40–U+2A4F], [U+2A51–U+2A63], {U+2ADB}, {U+2AF6}, {U+2AFB}, {U+2AFD},
|
B |
64 条(33 个 Unicode 范围)为infix 形式:
{U+0025}, {U+002A}, {U+002E}, [U+003F–U+0040], {U+005E}, {U+00B7}, {U+00D7}, {U+0323}, {U+032E}, {U+2022}, {U+2043}, [U+2217–U+2219], {U+2240}, {U+2297}, [U+2299–U+229B], [U+22A0–U+22A1], {U+22BA}, [U+22C4–U+22C7], [U+22C9–U+22CC], [U+2305–U+2306], {U+27CB}, {U+27CD}, [U+29C6–U+29C8], [U+29D4–U+29D7], {U+29E2}, [U+2A1D–U+2A1E], [U+2A2F–U+2A37], [U+2A3B–U+2A3D], {U+2A3F}, {U+2A50}, [U+2A64–U+2A65], [U+2ADC–U+2ADD], {U+2AFE},
|
C |
52 条(22 个 Unicode 范围)为prefix 形式:
{U+0021}, {U+002B}, {U+002D}, {U+00AC}, {U+00B1}, {U+0331}, {U+2018}, {U+201C}, [U+2200–U+2201], [U+2203–U+2204], {U+2207}, [U+2212–U+2213], [U+221F–U+2222], [U+2234–U+2235], {U+223C}, [U+22BE–U+22BF], {U+2310}, {U+2319}, [U+2795–U+2796], {U+27C0}, [U+299B–U+29AF], [U+2AEC–U+2AED],
|
D |
40 条(21 个 Unicode 范围)为postfix 形式:
[U+0021–U+0022], [U+0025–U+0027], {U+0060}, {U+00A8}, {U+00B0}, [U+00B2–U+00B4], [U+00B8–U+00B9], [U+02CA–U+02CB], [U+02D8–U+02DA], {U+02DD}, {U+0311}, {U+0320}, {U+0325}, {U+0327}, {U+0331}, [U+2019–U+201B], [U+201D–U+201F], [U+2032–U+2037], {U+2057}, [U+20DB–U+20DC], {U+23CD},
|
E |
30 条(prefix):
U+0028, U+005B, U+007B, U+007C, U+2016, U+2308, U+230A, U+2329, U+2772, U+27E6, U+27E8, U+27EA, U+27EC, U+27EE, U+2980, U+2983, U+2985, U+2987, U+2989, U+298B, U+298D, U+298F, U+2991, U+2993, U+2995, U+2997, U+2999, U+29D8, U+29DA, U+29FC,
|
F |
30 条(postfix):
U+0029, U+005D, U+007C, U+007D, U+2016, U+2309, U+230B, U+232A, U+2773, U+27E7, U+27E9, U+27EB, U+27ED, U+27EF, U+2980, U+2984, U+2986, U+2988, U+298A, U+298C, U+298E, U+2990, U+2992, U+2994, U+2996, U+2998, U+2999, U+29D9, U+29DB, U+29FD,
|
G |
27 条(2 个 Unicode 范围)为prefix 形式:
[U+222B–U+2233], [U+2A0B–U+2A1C],
|
H |
22 条(13 个 Unicode 范围)为postfix 形式:
[U+005E–U+005F], {U+007E}, {U+00AF}, [U+02C6–U+02C7], {U+02C9}, {U+02CD}, {U+02DC}, {U+02F7}, {U+0302}, {U+203E}, [U+2322–U+2323], [U+23B4–U+23B5], [U+23DC–U+23E1],
|
I |
22 条(6 个 Unicode 范围)为prefix 形式:
[U+220F–U+2211], [U+22C0–U+22C3], [U+2A00–U+2A0A], [U+2A1D–U+2A1E], {U+2AFC}, {U+2AFF},
|
J |
8 条(5 个 Unicode 范围)为infix 形式:
{U+002F}, {U+005C}, {U+005F}, [U+2061–U+2064], {U+2206},
|
K |
6 条(3 个 Unicode 范围)为prefix 形式:
[U+2145–U+2146], {U+2202}, [U+221A–U+221C],
|
L |
3 条(infix): U+002C, U+003A, U+003B, |
M |