CSS 变换模块第 2 级

1. 介绍

本规范是一个增量规范，它扩展了 [css-transforms-1]，允许作者在三维空间中变换元素。为 transform 属性添加的新变换函数允许三维变换，额外的属性使处理三维变换更加容易，并允许作者控制嵌套的三维变换元素如何交互。

perspective 属性允许作者为子元素提供额外的透视变换。perspective-origin 属性提供了对应用透视时的原点的控制，有效地改变了“消失点”的位置。
transform-style 属性允许 3D 变换元素及其 3D 变换的后代共享一个公共的三维空间，从而构建三维对象的层次结构。
backface-visibility 属性在通过三维变换将元素翻转过来使其背面可见时发挥作用。在某些情况下，隐藏该元素是可取的，可以使用此属性的 hidden 值实现。

注意：虽然一些 transform 属性的值允许在三维坐标系统中变换元素，但这些元素本身并不是三维对象。它们存在于二维平面（平面表面）上，没有深度。

本规范还添加了三个便利属性，scale、translate 和 rotate，使描述和动画化简单变换更加容易。

1.1. 模块交互

此处的3D变换函数扩展了transform属性的函数集。

perspective、transform-style 和 backface-visibility 的一些值会导致创建所有后代的包含块，或创建堆叠上下文。

三维变换影响元素的视觉层次，因此会覆盖附录E中描述的自后向前的绘制顺序，参见 [CSS21]。

1.2. 值定义

本规范遵循 CSS 属性定义约定，来源于 [CSS21]，使用值定义语法，来源于 [CSS-VALUES-3]。未在本规范中定义的值类型定义在CSS值与单位模块 [CSS-VALUES-3]中。与其他CSS模块结合可能会扩展这些值类型的定义。

除了在各自定义中列出的特定于属性的值外，本规范中定义的所有属性还接受 CSS-wide 关键字作为其属性值。为了提高可读性，它们没有被明确重复。

2. 术语

3D 变换元素: 其 transform 属性的计算值包含一个 3D 变换函数的元素。
3D 矩阵: 一个 4x4 矩阵，不符合 2D 矩阵的要求。
单位变换函数: 除了 CSS Transforms 中的单位变换函数之外，单位变换函数的示例还包括 translate3d(0, 0, 0)、translateZ(0)、scaleZ(1)、rotate3d(1, 1, 1, 0)、rotateX(0)、rotateY(0)、rotateZ(0) 和 matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)。特殊情况是 perspective: perspective(none)。 m₃₄ 的值变得极小，因此假设该变换函数等同于单位矩阵。
透视矩阵: 根据 perspective 和 perspective-origin 属性的值计算得出的矩阵，如下文所述。
累积 3D 变换矩阵: 为元素相对于其 3D 渲染上下文的根计算的矩阵，如下文所述。
3D 渲染上下文: 一组具有共同祖先的元素，它们共享一个共同的三维坐标系统，如下文所述。

2.1. 计算值的 <transform-list> 序列化

为 <transform-list> 的计算值将根据以下算法序列化为 <matrix()> 或 <matrix3d()> 函数：

让 transform 为一个初始化为单位矩阵的 4x4 矩阵。transform 的元素 m11、m22、m33 和 m44 必须设置为 1，transform 的所有其他元素必须设置为 0。
将 <transform-function> 中的所有 <transform-list> 后乘到 transform。
在 <matrix()> 和 <matrix3d()> 序列化之间进行选择：

如果 transform 是 2D 矩阵
将 transform 序列化为 <matrix()> 函数。
否则
将 transform 序列化为 <matrix3d()> 函数。

修正此文本以添加到 CSS Transforms 1 中的文本。

3. 二维子集

UA 可能并不总是能够渲染三维变换，而只是支持该规范的二维子集。在这种情况下，三维变换和 transform-style，perspective，perspective-origin 和 backface-visibility 必须不被支持。3D 变换渲染不适用。矩阵分解使用的是 "Graphics Gems II, edited by Jim Arvo" 中 "unmatrix" 方法的简化版本，适用于 2D 情况。变换函数的数学描述仍然有效，但可以通过使用 3x3 变换矩阵来简化，其中 a 等于 m₁₁，b 等于 m₁₂，c 等于 m₂₁，d 等于 m₂₂，e 等于 m₄₁，f 等于 m₄₂（参见具有六个参数的 2D 3x2 矩阵）。

$$\begin{bmatrix} a & c & e \\ b & d & f \\ 0 & 0 & 1 \end{bmatrix}$$

用于二维变换的 3x3 矩阵。

如果 UA 不支持三维变换，作者可以轻松提供回退方案。以下示例有两个 transform 属性定义。第一个由两个二维变换函数组成，第二个包含一个二维和一个三维变换函数。

div {  transform: scale(2) rotate(45deg);
  transform: scale(2) rotate3d(0, 0, 1, 45deg);
}

如果支持 3D，第二个定义会覆盖第一个定义。如果不支持 3D，第二个定义无效，UA 会回退到第一个定义。

4. 变换渲染模型

本规范扩展了 CSS Transforms 1 § 3 变换渲染模型，以适应三维变换函数、transform-origin 的 Z 值、perspective 属性以及在 transform-style 属性的使用值为 preserve-3d 时适用的新 3D 渲染模型。

三维变换函数从概念上将坐标空间扩展为三维，增加了一个与屏幕平面垂直的 Z 轴，该轴朝向观察者增加。

初始坐标空间的演示。

使用 3D 变换时，transform-origin 的 Z 组件会影响结果，因此变换矩阵是根据 transform 和 transform-origin 属性计算得出的，具体步骤如下：

从单位矩阵开始。
通过计算出的 transform-origin 的 X、Y 和 Z 进行平移。
从左到右依次乘以 transform 属性中的每个变换函数。
通过 transform-origin 的计算出的 X、Y 和 Z 的相反值进行平移。

4.1. 3D 变换渲染

通常，元素以平面形式呈现，并被渲染到与其堆叠上下文相同的平面中。这通常是与页面其他部分共享的平面。二维变换函数可以改变元素的外观，但该元素仍然被渲染到与其堆叠上下文相同的平面中。

未包含在 3D 渲染上下文中的三维变换元素，应用适当的变换后进行渲染，但不会与其他元素相交。在这种情况下，三维变换可以被视为类似二维变换的绘制效果。同样，变换不会影响绘制顺序。例如，具有正 Z 平移的变换可能会使元素看起来更大，但不会使该元素在没有 Z 平移的元素前面渲染。

描述嵌套的 3D 变换元素如何渲染（可能需要使用数学描述）

本示例与前述文本不相关。

该示例展示了应用三维变换后的效果。

<style>
div {
    height: 150px;
    width: 150px;
}
.container {
    border: 1px solid black;
}
.transformed {
    transform: rotateY(50deg);
}
</style>

<div class="container">
    <div class="transformed"></div>
</div>

该变换是围绕垂直 Y 轴的 50° 旋转。注意，这使蓝色框看起来变窄了，但不是三维的。

4.1.1. 透视

透视可以用于为场景添加深度感，使得在 Z 轴上更靠近观察者的元素显得更大，而更远的元素则显得更小。缩放比例与 d/(d − Z) 成正比，其中 d 是 perspective 的值，表示从绘图平面到假定的观察者眼睛位置的距离。

透视效果可以通过两种方式应用于 3D 变换元素。首先，元素的 '变换函数列表' 中可以包含 perspective() 函数，该函数会计算到元素的 '当前变换矩阵' 中。

其次，可以将 perspective 和 perspective-origin 属性应用于元素，以影响其 3D 变换的子元素的渲染，使它们共享一个共同的透视效果，从而产生它们处于同一三维场景中的印象。

此图显示了缩放如何取决于 perspective 属性和 Z 位置。在上图中，Z 是 d 的一半。为了使原始圆（实线轮廓）看起来位于 Z 位置（虚线圆），圆会被放大两倍，结果是浅蓝色圆。在下图中，圆被缩小到原来的三分之一，看起来位于原始位置之后。

通常，假定观察者的眼睛位置在绘图的中心。可以根据需要移动此位置，例如当网页包含多个应共享共同透视的绘图时，可以通过设置 perspective-origin 实现。

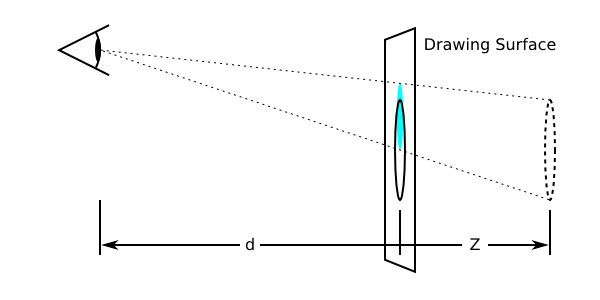
此图展示了将透视原点上移的效果。

透视矩阵的计算方式如下：

从单位矩阵开始。
通过 perspective-origin 的计算出的 X 和 Y 值进行平移。
乘以 perspective() 变换函数生成的矩阵，其中长度由 perspective 属性的值提供。
通过 perspective-origin 的计算出的 X 和 Y 的相反值进行平移。

该示例展示了如何使用透视使三维变换看起来更加逼真。

<style>
div {
  height: 150px;
  width: 150px;
}
.container {
  perspective: 500px;
  border: 1px solid black;
}
.transformed {
  transform: rotateY(50deg);
}
</style>

<div class="container">
  <div class="transformed"></div>
</div>

内部元素与前一个示例具有相同的变换，但其渲染现在受其父元素上的 perspective 属性影响。透视效果使具有正 Z 坐标（靠近观察者）的顶点在 X 和 Y 方向上放大，而远离观察者（负 Z 坐标）的顶点缩小，从而产生深度感。

4.1.2. 3D 渲染上下文

本节指定了使用 3D 变换和 transform-style 属性的内容的渲染模型。为了描述此模型，我们引入了“3D 渲染上下文”的概念。

3D 渲染上下文是一个以共同祖先为根的元素集合，出于 3D 变换渲染的目的，它们被视为共享一个三维坐标系统。在 3D 渲染上下文中的元素的前后渲染取决于它们在三维空间中的 z 位置，并且如果这些元素上的 3D 变换导致它们相交，它们会带有相交效果进行渲染。

每个元素在该三维空间中的位置是通过从给定元素到建立 3D 渲染上下文的元素逐级累加变换矩阵来确定的。

元素通过以下方式建立并参与 3D 渲染上下文：

由 3D 渲染上下文创建的元素是一个可变换的元素，其 transform-style 的使用值为 preserve-3d，且它本身不是 3D 渲染上下文的一部分。创建 3D 渲染上下文的元素也参与该上下文。
一个元素的 transform-style 的使用值为 preserve-3d 且它本身参与了 3D 渲染上下文，则扩展该 3D 渲染上下文，而不是创建新的上下文。
如果元素的父元素创建或扩展了一个 3D 渲染上下文，则该元素参与该 3D 渲染上下文。

某些 CSS 属性具有被视为强制“分组”的值：它们要求元素及其后代作为一个整体在与其他元素合成之前进行渲染；这些包括不透明度、滤镜以及影响裁剪的属性。相关的属性值列在分组属性值下。因此，当它们用于带有 transform-style:preserve-3d 的元素时，它们会将使用值更改为 flat，并阻止其创建或扩展 3D 渲染上下文。

在 3D 渲染上下文中，元素的渲染和排序如下进行：

创建 3D 渲染上下文的元素以及参与 3D 渲染上下文的其他 3D 变换元素将被渲染到它们自己的平面中。该平面包括元素的背景、边框、其他框装饰、内容以及后代元素，但不包括任何具有自己平面的后代元素（及其后代）。此渲染是按照 CSS 2.1, 附录 E, 第 E.2 节绘制顺序进行的。
该平面集合按照 Newell 算法执行相交操作，平面会根据累加的 3D 变换矩阵进行变换。共面的 3D 变换元素按照绘制顺序渲染。

是否可以不将 2D 变换的元素弹出到它们自己的平面中？

注意：该规范之前定义了创建元素的背景、边框和其他框装饰会在整个 3D 场景后面进行渲染。在 #6238 中对此进行了更改。但是，如果未来 3D 渲染上下文的定义发生更改，可能需要考虑恢复此定义。

注意，具有负 z 分量变换的元素将会在创建元素的内容和未变换的后代后面渲染，并且 3D 变换元素可能与内容和未变换的元素相互渗透。

注意：因为 3D 渲染上下文中的 3D 变换元素可以彼此进行深度排序和相交，所以它们实际上是像兄弟姐妹一样渲染的。因此，transform-style: preserve-3d 的效果可以理解为将 3D 渲染上下文中的所有 3D 变换元素提升到创建元素中，但仍然使用它们的累加 3D 变换矩阵进行渲染。

<style>
div {
  height: 150px;
  width: 150px;
}
.scene {
  background-color: rgba(0, 0, 0, 0.3);
  border: 1px solid black;
  perspective: 500px;
}
.container {
  transform-style: preserve-3d;
}
.container > div {
  position: absolute;
  left: 0;
}
.container > :first-child {
  transform: rotateY(45deg);
  background-color: orange;
  top: 10px;
  height: 135px;
}
.container > :last-child {
  transform: translateZ(40px);
  background-color: rgba(0, 0, 255, 0.6);
  top: 50px;
  height: 100px;
}
</style>

<div class="scene">
  <div class="container">
    Lorem ipsum dolor sit amet, consectetaur adipisicing elit…
    <div></div>
    <div></div>
  </div>
</div>

此示例展示了 3D 渲染上下文中的元素如何相交。容器元素为自身及其两个子元素创建了一个 3D 渲染上下文，场景元素为 3D 渲染上下文添加了透视效果。子元素相互交叉，橙色元素也与容器相交。

<style>
div {
  height: 150px;
  width: 150px;
}
.container {
  perspective: 500px;
  border: 1px solid black;
}
.transformed {
  transform: rotateY(50deg);
  background-color: blue;
}
.child {
  transform-origin: top left;
  transform: rotateX(40deg);
  background-color: lime;
}
</style>

<div class="container">
  <div class="transformed">
    <div class="child"></div>
  </div>
</div>

此示例展示了嵌套的 3D 变换如何渲染。蓝色 div 的变换与上一个示例中的相同，其渲染受到其父元素上的透视影响。绿色元素也具有 3D 变换，这是绕 X 轴的旋转（锚定在顶部，归因于 transform-origin）。然而，绿色元素正在平坦化为父元素的平面，因为它不是同一个 3D 渲染上下文的成员。因此，绿色元素只是看起来变得更短；它并没有从蓝色元素中“弹出”。

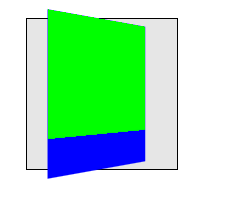
4.1.3. 变换元素层次结构

默认情况下，变换元素不会创建3D 渲染上下文，并且会创建其内容的平坦表示。然而，由于构建共享共同三维空间的变换对象层次结构是有用的，可以通过为 transform-style 属性指定 preserve-3d 的值来覆盖此平坦化行为。这允许变换元素的后代共享相同的 3D 渲染上下文。此类元素的非 3D 变换后代将在上面步骤 C 中的平面中渲染，但同一 3D 渲染上下文中的 3D 变换元素将“弹出”到它们自己的平面中。

<style>
div {
  height: 150px;
  width: 150px;
}
.container {
  perspective: 500px;
  border: 1px solid black;
}
.transformed {
  transform-style: preserve-3d;
  transform: rotateY(50deg);
  background-color: blue;
}
.child {
  transform-origin: top left;
  transform: rotateX(40deg);
  background-color: lime;
}
</style>

该示例与前一个示例相同，增加了在蓝色元素上使用的 transform-style: preserve-3d。蓝色元素现在扩展了其容器的 3D 渲染上下文。现在蓝色和绿色元素共享一个共同的三维空间，因此绿色元素渲染时倾斜出其父元素，并受到容器上的透视影响。

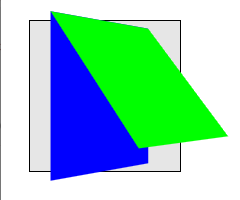
4.1.4. 累加的 3D 变换矩阵计算

在 3D 渲染上下文中用于渲染元素的最终变换值通过累加累加的 3D 变换矩阵进行计算，步骤如下：

令 transform 为单位矩阵。
令 当前元素 为变换元素。
令 父元素 为变换元素的父元素。
当 当前元素 是其 3D 渲染上下文中的元素时：
1. 如果 当前元素 的 transform 值不是 none，则将 当前元素 的变换矩阵与 transform 进行前乘。
2. 计算表示 当前元素 相对于 父元素 的偏移（包括滚动偏移）的平移矩阵，并将该矩阵与 transform 进行前乘。
3. 如果 父元素 的 perspective 值不是 none，则将 父元素 的透视矩阵与 transform 进行前乘。
4. 令 当前元素 为 父元素。
5. 令 父元素 为 当前元素 的父元素。

注意：如此处所述，累加的 3D 变换矩阵考虑了由视觉格式化模型在变换元素及其祖先链中的元素（包括建立其 3D 渲染上下文的元素）上生成的偏移（包括滚动偏移）。

4.1.5. 反面可见性

通过使用三维变换，可以将元素变换为使其背面可见的状态。3D 变换元素在两侧显示相同的内容，因此背面看起来像是正面的镜像（好像元素被投影到一块玻璃上）。通常，背面朝向观看者的元素仍然可见。然而，backface-visibility 属性允许作者使背面朝向观看者时的元素不可见。这种行为是“实时”的；如果具有 backface-visibility: hidden 的元素正在动画中，且正反两面交替可见，那么它只会在正面朝向观看者时可见。

元素背面的可见性是通过累加的 3D 变换矩阵进行判断的，因此是相对于创建 3D 渲染上下文的元素的父元素而言的。

注意：此属性在将两个元素背靠背放置时非常有用，例如创建一张扑克牌。没有此属性，在动画翻牌过程中，正面和背面元素可能会调换位置。另一个示例是使用 6 个元素创建一个盒子，但您希望只看到盒子的内侧面。

此示例展示了如何制作在点击时翻转的“卡片”元素。请注意 #card 上的 "transform-style: preserve-3d"，这对于避免翻转时的平坦化是必要的。

<style>
.body { perspective: 500px; }
#card {
  position: relative;
  height: 300px; width: 200px;
  transition: transform 1s;
  transform-style: preserve-3d;
}
#card.flipped {
  transform: rotateY(180deg);
}
.face {
  position: absolute;
  top: 0; left: 0;
  width: 100%; height: 100%;
  background-color: silver;
  border-radius: 40px;
  backface-visibility: hidden;
}
.back {
  transform: rotateY(180deg);
}
</style>
<div id="card" onclick="this.classList.toggle('flipped')">
  <div class="front face">Front</div>
  <div class="back face">Back</div>
</div>

backface-visibility 对非变换或二维变换元素有什么影响？这些元素是否会被弹出到它们自己的平面并发生相交？

4.2. 透视变换盒的处理

这是首次尝试精确指定如何使用提供的矩阵来变换元素的初步尝试。它可能不是理想的，并鼓励实现者提供反馈。详见 #912。

累积的三维变换矩阵受 perspective 属性和 transform 属性中的任何 perspective() 变换函数影响。

该累积的三维变换矩阵是一个4×4矩阵，而要变换的对象是二维盒子。为了变换盒子的每个角(a, b)，首先需要将矩阵应用于(a, b, 0, 1)，结果将得到四维点(x, y, z, w)。然后将其转换为三维点(x′, y′, z′)，具体如下：

如果 w > 0, (x′, y′, z′) = (x/w, y/w, z/w)。

如果 w = 0, (x′, y′, z′) = (x ⋅ n, y ⋅ n, z ⋅ n)。 n 是实现依赖的值，应选择使得 x′ 或 y′ 尽可能大于视口大小。例如，(5px, 22px, 0px, 0) 可能变为 (5000px, 22000px, 0px)，其中 n = 1000，但此值对于 (0.1px, 0.05px, 0px, 0) 来说可能太小。本规范未明确定义 n 的确切值。概念上，(x′, y′, z′) 在方向(x, y, z)上无限远。

如果 w < 0 且所有四个角点都小于 0，则该盒子不会被渲染。

如果 w < 0 且盒子的一个到三个角点小于 0，则必须将该盒子替换为一个多边形，去除 w < 0 的部分。通常这将是一个具有三到五个顶点的多边形，其中恰好有两个顶点的 w = 0，其余的 w > 0。这些顶点然后根据刚刚说明的规则转换为三维点。概念上，w < 0 的点是“在”观察者“后面”，因此不应可见。

.transformed {
  height: 100px;
  width: 100px;
  background: lime;
  transform: perspective(50px) translateZ(100px);
}

盒子的所有角的 z 坐标都大于透视值。这意味着盒子位于观察者的后方，不会显示。数学上，点 (x, y) 首先变为 (x, y, 0, 1)，然后平移到 (x, y, 100, 1)，接着应用透视变换后得到 (x, y, 100, −1)。由于 w 坐标为负值，因此它不会显示。如果实现没有单独处理 w < 0 的情况，可能会错误地显示该点为 (−x, −y, −100)，通过除以 −1 而镜像显示盒子。

.transformed {
  height: 100px;
  width: 100px;
  background: radial-gradient(yellow, blue);
  transform: perspective(50px) translateZ(50px);
}

在这里，盒子被向上平移，使其位于观察者正在看的位置。这就像将盒子越来越靠近眼睛，直到它填满整个视野。由于默认的 transform-origin 在盒子的中心（黄色），屏幕将被黄色填满。

从数学上讲，点 (x, y) 首先变为 (x, y, 0, 1)，然后平移到 (x, y, 50, 1)，再应用透视变换后变为 (x, y, 50, 0)。相对于位于中心的 transform-origin，左上角的坐标是 (−50, −50)，因此它变为 (−50, −50, 50, 0)。这个点被变换到一个非常远的左上方，例如 (−5000, −5000, 5000)。同样，其他角也被变换到非常远的地方。径向渐变在整个盒子上拉伸，变得非常大，因此在不滚动的情况下可见的部分应该是中间像素的颜色：黄色。然而，由于盒子实际上不是无限大的，用户仍然可以滚动到边缘看到蓝色部分。

.transformed {
  height: 50px;
  width: 50px;
  background: lime;
  border: 25px solid blue;
  transform-origin: left;
  transform: perspective(50px) rotateY(-45deg);
}

盒子将向观察者旋转，左边缘保持固定，而右边缘则会靠近。右边缘的 z 值大约是 70.7px，比 50px 的透视值更接近。因此，最右边的边缘将消失（"在"观察者后面），可见的部分将无限延伸到右边。

从数学上讲，盒子的右上顶点相对于 transform-origin 最初是 (100, −50)。首先扩展为 (100, −50, 0, 1)。应用指定的变换后，它将映射到大约 (70.71, −50, 70.71, −0.4142)。此时 w = −0.4142 < 0，因此我们需要切掉 w < 0 的部分。这将导致新的右上顶点为 (50, −50, 50, 0)。然后将其映射到相同方向的一个远处点，例如 (5000, −5000, 5000)，即从 transform-origin 往上右方延伸。类似的过程会发生在右下角，它将映射到右下方很远的地方。结果是盒子远远超出了屏幕的边缘。

再次强调，渲染的盒子仍然是有限的，用户可以滚动查看整个内容。然而，右边的部分已经被截断了。不管用户如何滚动，原始盒子最右边大约 30px 的部分将不可见。蓝色边框只有 25px 宽，所以它将在左边、顶部和底部可见，但不会在右边。

如果一个或三个顶点的 w < 0，那么相同的基本步骤也适用。但在这种情况下，截掉 w < 0 的部分将导致生成一个三角形或五边形，而不是四边形。

5. 单独的变换属性：translate、scale 和 rotate 属性

translate、rotate 和 scale 属性允许作者独立指定简单的变换，以符合典型用户界面使用方式，而不必记住 transform 的顺序，以确保 translate()、rotate() 和 scale() 的独立性，并作用于屏幕坐标。

名称：	translate
值：	none \| <length-percentage> [ <length-percentage> <length>? ]?
初始值：	none
适用于：	可变换元素
继承：	no
百分比：	相对于参考框的宽度（第一个值）或高度（第二个值）
计算值：	关键字 none 或一对计算的 <length-percentage> 值和一个绝对长度
规范顺序：	根据语法
动画类型：	按计算值，但请参阅下面的 none

translate 属性接受 1-3 个值，每个值分别指定沿一个轴的平移，按 X、Y 和 Z 顺序排列。当第二或第三个值缺失时，它们默认为 0px。

如果第三个值省略或为零，则指定一个二维平移，相当于 translate() 函数。否则，则指定一个三维平移，相当于 translate3d() 函数。

注意：解析值的 translate 属性是计算值，因此 getComputedStyle() 会在其结果中包括百分比值。

名称：	rotate
值：	none \| <angle> \| [ x \| y \| z \| <number>{3} ] && <angle>
初始值：	none
适用于：	可变换元素
继承：	no
百分比：	不适用
计算值：	关键字 none 或带有三元轴的 <angle> 和包含三个 <number> 值的轴
规范顺序：	根据语法
动画类型：	SLERP 方式，但请参阅下方的 none

rotate 属性接受一个用于旋转元素的角度，以及可选的一个旋转轴。

旋转轴可以通过 x、y，或 z 关键字指定，这些关键字分别指定围绕对应轴的旋转，相当于 rotateX()、rotateY()、和 rotateZ() 变换函数。另外，轴也可以通过显式提供三个数值来指定，这三个数值代表一个以原点为中心的向量的 x、y 和 z 分量，相当于 rotate3d() 函数。

在行为上没有区别，无论是仅指定为 <angle> 的旋转，还是围绕 z 轴指定的旋转（无论是通过 z 关键字，还是通过向量的前两个分量为零、第三个分量为正来指定）；它们都是相当于 rotate() 函数的二维旋转。例如，rotate: 30deg，rotate: z 30deg，以及 rotate: 0 0 1 30deg 都是等效的。

名称：	scale
值：	none \| [ <number> \| <percentage> ]{1,3}
初始值：	none
适用于：	可变换元素
继承：	no
百分比：	不适用
计算值：	关键字 none 或一个带有三个 <number> 的列表
规范顺序：	根据语法
动画类型：	按计算值，但参阅下方的 none

scale 属性接受1-3个值，每个值分别指定沿一个轴的缩放比例，顺序为 X，Y，然后是 Z。

如果没有给定 Y 值，则默认为与 X 值相同。

如果没有给定 Z 值，则默认为 1。

如果第三个值被省略，或为 1 或 100%，则这指定的是二维缩放，相当于 scale() 函数。否则，则这指定的是三维缩放，相当于 scale3d() 函数。

第三个值被省略时的行为与其为 1 或 100% 时没有区别。

<percentage> 等同于 <number>，例如 scale: 100% 等同于 scale: 1。数值用于指定和计算值的序列化。

这三个属性都接受（并默认）值 none，这不产生任何变换。特别地，该值不会触发堆叠上下文或所有后代元素的包含块的创建，而所有其他值（包括 “identity” 变换如 translate: 0px）按变换的常规情况创建堆叠上下文和所有后代元素的包含块。

当 translate、rotate 或 scale 正在进行动画或过渡时，且 from 值或 to 值（但不是两者都）是 none，则 none 值将被等效的 identity 值替代（0px 对于 translate，0deg 对于 rotate，1 对于 scale）。

5.1. 序列化

由于这些属性有两种截然不同的行为模式（无变换和有变换），序列化必须考虑到这一点：

针对 translate

如果指定了平移，则该属性必须以一到三个值进行序列化。（通常，如果第二和第三个值是 0px，默认值，或者只有第三个值是 0px，那么这些 0px 值在序列化时必须省略）。

只有当原本指定了 none 时，才必须序列化为关键字 none。（单位变换不算；它必须序列化为 0px。）

针对 rotate

如果指定了绕 Z 轴旋转（即二维中的旋转），则该属性必须仅序列化为一个 <angle>。

如果指定了其他旋转，则该属性必须以指定的轴进行序列化。如果该轴与 x 轴或 y 轴平行，它必须序列化为适当的关键字。

只有当原本指定了 none 时，才必须序列化为关键字 none。（单位变换不算；它必须序列化为 0deg。）

针对 scale

如果指定了缩放，则该属性必须仅以一到三个值进行序列化。通常，如果第三个值为1（默认值），则序列化时会省略它。如果第三个值被省略且第二个值与第一个值相同（默认值），则序列化时也会省略第二个值。

只有当原本指定了 none 时，才必须序列化为关键字 none。（单位变换不算；它必须序列化为 1。）

6. 当前变换矩阵

对变换矩阵计算进行如下修正：

变换矩阵从 transform、transform-origin、translate、rotate、scale 和 offset 属性计算如下：

从单位矩阵开始。
根据 transform-origin 的计算 X、Y 和 Z 值进行平移。
根据 translate 的计算 X、Y 和 Z 值进行平移。
围绕 rotate 的指定轴，按计算的 <angle> 进行旋转。
按 scale 的计算 X、Y 和 Z 值进行缩放。
根据 offset 指定的变换进行平移和旋转。
按从左到右的顺序，逐一乘以 transform 中的变换函数。
按 transform-origin 的计算 X、Y 和 Z 值的负值进行平移。

7. transform-style 属性

名称:	transform-style
值:	flat \| preserve-3d
初始值:	flat
适用范围:	可变换元素
是否继承:	否
百分比:	不适用
计算值:	指定的关键字
规范顺序:	按照语法
动画类型:	离散
使用值:	如果存在分组属性，则为 flat，否则为指定的关键字

对于 transform-style 的计算值为 preserve-3d 的可变换元素，它同时建立堆叠上下文和所有后代的包含块。如果使用值为 preserve-3d，那么它也会建立或扩展 3D 渲染上下文。

7.1. 分组属性值

以下 CSS 属性值要求用户代理在应用它们之前创建后代元素的扁平化表示，因此强制元素的 preserve-3d 使用样式为 flat。

overflow: 任何值，除了 visible 或 clip。
opacity: 任何小于 1 的值。
filter: 任何值，除了 none。
clip: 任何值，除了 auto。
clip-path: 任何值，除了 none。
isolation: 使用值为 isolate。
mask-image: 任何值，除了 none。
mask-border-source: 任何值，除了 none。
mix-blend-mode: 任何值，除了 normal。
contain: paint 以及任何导致绘制包含的其他属性/值组合。注意：这包括任何影响使用值的属性，如 content-visibility: hidden。

8. perspective 属性

名称:	perspective
值:	none \| <length [0,∞]>
初始值:	none
适用范围:	可变换元素
是否继承:	否
百分比:	不适用
计算值:	关键词 none 或一个绝对长度值
规范顺序:	根据语法
动画类型:	根据计算值

<length [0,∞]>

到投影中心的距离。

验证投影是否为到投影中心的距离。

由于非常小的 <length> 值会产生奇怪的渲染结果并对变换计算的数值精度造成压力，小于 1px 的值在渲染时必须视为 1px。（此限制不会影响底层值，因此样式表中的 perspective: 0; 仍然会序列化回 0。）

none

不应用透视变换。效果在数学上类似于无限大的 <length> 值。所有对象看起来都在画布上是平的。

此属性使用除 none 以外的任何值时会建立堆叠上下文。它还会像 transform 属性一样建立所有后代的包含块。

我们不需要为透视建立堆叠上下文或包含块，但可能由于网页兼容性问题，无法改变这一点。

perspective 和 perspective-origin 属性的值用于计算透视矩阵，如上所述。

9. perspective-origin 属性

perspective-origin 属性确定了 perspective 属性的原点。它有效地设置了观察者看待元素子项的位置，即 X 和 Y 位置。

名称:	perspective-origin
值:	<position>
初始值:	50% 50%
适用范围:	可变换元素
是否继承:	否
百分比:	相对于参考框的大小
计算值:	参见 background-position
规范顺序:	按语法
动画类型:	根据计算值

perspective 和 perspective-origin 属性的值用于计算透视矩阵，如上所述。

perspective-origin 的值表示从参考框左上角开始的偏移量。

<percentage>: 水平透视偏移的百分比相对于参考框的宽度。垂直偏移的百分比相对于参考框的高度。水平和垂直偏移的值表示从参考框左上角开始的偏移量。
<length>: 长度值给出了一个固定的偏移长度。水平和垂直偏移的值表示从参考框左上角开始的偏移量。
top: 如果给定了一个或两个值，计算为垂直位置的 0%，否则指定上边缘为下一个偏移的起点。
right: 如果给定了一个或两个值，计算为水平位置的 100%，否则指定右边缘为下一个偏移的起点。
bottom: 如果给定了一个或两个值，计算为垂直位置的 100%，否则指定下边缘为下一个偏移的起点。
left: 如果给定了一个或两个值，计算为水平位置的 0%，否则指定左边缘为下一个偏移的起点。
center: 如果水平位置没有指定，计算为 50% (left 50%)，或者如果没有指定垂直位置，则计算为 50% (top 50%)。

perspective-origin 属性是一个解析值特殊情况属性，类似于 height。[CSSOM]

10. backface-visibility 属性

名称:	backface-visibility
值:	visible \| hidden
初始值:	visible
适用范围:	可变换元素
是否继承:	否
百分比:	N/A
计算值:	指定的关键字
规范顺序:	按语法
动画类型:	离散型

具有 backface-visibility: hidden 的元素的可见性如下确定：

计算元素的累积 3D 变换矩阵。
如果矩阵中第 3 行第 3 列的分量为负数，则元素应被隐藏。否则可见。

backface-visibility 不能仅通过查看 m33 进行测试。请参阅 #917。

注意：该定义的推理如下。假设元素是位于 x–y 平面中的矩形，具有无限小的厚度。未变换的元素的正面坐标为 (x, y, ε)，背面为 (x, y, −ε)，其中 ε 非常小。我们希望知道在变换后，元素的正面是比背面更接近观察者（更高的 z 值）还是更远。正面的 z 坐标为 m₁₃x + m₂₃y + m₃₃ε + m₄₃，背面则为 m₁₃x + m₂₃y − m₃₃ε + m₄₃。当且仅当 m₃₃ > 0 时，前者大于后者。（如果等于零，则正面和背面距离观察者一样近。这可能意味着发生了类似 90 度旋转的情况，这样元素本身就是不可见的，因此我们不太关心它是否会消失。）

11. SVG 和 3D 变换函数

本规范明确要求三维变换函数适用于以下容器元素: a, g, svg, 所有图形元素, 所有图形引用元素以及 SVG 的 foreignObject 元素。

三维变换函数和属性 perspective, perspective-origin, transform-style 以及 backface-visibility 不能用于以下元素: clipPath, linearGradient, radialGradient 以及 pattern。如果变换列表中包含三维变换函数，则必须忽略完整的变换列表。之前提到的所有属性的值都必须忽略。包含在这些元素中的可变换元素可以使用三维变换函数。 clipPath, mask, pattern 元素要求用户代理在应用它们之前创建后代元素的平面表示，因此会覆盖 transform-style: preserve-3d 的行为。

如果 vector-effect 属性设置为 non-scaling-stroke 并且对象处于 3D 渲染上下文中，则该属性对描边对象没有影响。

正式描述 SVG 中 3D 变换函数的语法，如 2D 函数的语法所示。

12. 变换函数

transform 属性的值是 <transform-function> 列表。允许的变换函数集如下所示。任何地方使用 <angle> 时，0 等于 0 度，也可以使用 <number>，并视为与零度相同。水平平移的百分比相对于参考框的宽度，垂直平移的百分比相对于参考框的高度。缩放函数中的百分比等同于数字，在指定值中以数字形式序列化。例如，scale3d(50%, 100%, 150%) 序列化为 scale3d(0.5, 1, 1.5)。

12.1. 2D 变换函数

在 [css-transforms-1] 中定义的缩放函数现在支持百分比。

scale() = scale( [ <number> | <percentage> ]#{1,2} )
scaleX() = scaleX( [ <number> | <percentage> ] )
scaleY() = scaleY( [ <number> | <percentage> ] ): 如 css-transforms-1 中定义，但也接受百分比，如上文所述。

12.2. 3D 变换函数

在以下 3d 变换函数中，<zero> 与 0deg 相同。（“无单位的 0” 角度保留是为了兼容旧版。）

matrix3d() = matrix3d( <number>#{16} )

指定一个 4x4 齐次矩阵的 3D 变换，按列优先顺序排列 16 个值。

translate3d() = translate3d( <length-percentage> , <length-percentage> , <length> )

指定一个 3D 平移，由向量 [tx,ty,tz] 描述，tx、ty 和 tz 分别是三个平移值参数。

translateZ() = translateZ( <length> )

指定一个 3D 平移，由向量 [0,0,tz] 描述，沿 Z 方向平移。

scale3d() = scale3d( [ <number> | <percentage> ]#{3} )

指定一个 3D 缩放操作，由 [sx,sy,sz] 缩放向量描述。

scaleZ() = scaleZ( [ <number> | <percentage> ] )

指定一个 3D 缩放操作，使用 [1,1,sz] 缩放向量，其中 sz 为参数。

rotate3d() = rotate3d( <number> , <number> , <number> , [ <angle> | <zero> ] )

指定一个 3D 旋转，由最后一个参数指定角度，围绕由前三个参数描述的 [x,y,z] 方向向量旋转。如果方向向量无法归一化，例如 [0,0,0]，则旋转不适用。

注意：旋转方向是顺时针，观察点位于向量末端并朝向原点。

rotateX() = rotateX( [ <angle> | <zero> ] )

等同于 rotate3d(1, 0, 0, <angle>)。

rotateY() = rotateY( [ <angle> | <zero> ] )

等同于 rotate3d(0, 1, 0, <angle>)。

rotateZ() = rotateZ( [ <angle> | <zero> ] )

等同于 rotate3d(0, 0, 1, <angle>)，这是与 2d 变换 rotate(<angle>) 等效的 3d 变换。

perspective() = perspective( <length [0,∞]> | none )

指定一个透视投影矩阵。该矩阵基于 Z 值缩放 X 和 Y 方向上的点，使得正 Z 值的点远离原点，负 Z 值的点向原点移动。z=0 平面的点不受影响。参数表示 z=0 平面与观察者的距离。较小的值给出更扁平的金字塔形状，从而产生更明显的透视效果。例如，1000px 的值提供适度的缩短效果，而 200px 的值提供极端的透视效果。

如果深度值小于 1px，则在渲染时必须将其视为 1px，用于计算解析值或 transform，以及作为插值的端点时使用。

注意：上述关于小于 1px 值的规则，旨在涵盖 perspective() 函数需要转换为矩阵的情况。

12.3. 变换函数原语和衍生函数

某些变换函数可以由更通用的变换函数表示。这些变换函数称为衍生变换函数，而通用的变换函数称为原始变换函数。三维原始函数及其衍生变换函数包括：

translate3d(): 适用于 <translateX()>、<translateY()>、translateZ() 和 <translate()>。
scale3d(): 适用于 <scaleX()>、<scaleY()>、scaleZ() 和 <scale()>。
rotate3d(): 适用于 <rotate()>、rotateX()、rotateY() 和 rotateZ()。

对于具有二维原语和三维原语的衍生变换函数，使用的原语由上下文决定。参见原语和衍生变换函数的插值。

13. 矩阵的插值

在两个矩阵之间进行插值时，每个矩阵都会分解为相应的平移、旋转、缩放、倾斜和（对于三维矩阵）透视值。每个分解矩阵的对应部分以数值方式插值，并在最后一步重新组合回矩阵。

13.1. 三维矩阵的插值

13.1.1. 分解三维矩阵

以下伪代码基于“Graphics Gems II，Jim Arvo 编辑”的“unmatrix”方法，但修改为使用四元数而非欧拉角，以避免万向节锁问题。

以下伪代码适用于 4x4 齐次矩阵：

输入:  matrix      ; 一个4x4矩阵
输出: translation ; 一个3维向量
        scale       ; 一个3维向量
        skew        ; XY、XZ、YZ倾斜因子表示为3维向量
        perspective ; 一个4维向量
        quaternion  ; 一个4维向量
如果矩阵不能分解，返回false；如果可以分解，返回true


// 归一化矩阵。
if (matrix[3][3] == 0)
    return false

for (i = 0; i < 4; i++)
    for (j = 0; j < 4; j++)
        matrix[i][j] /= matrix[3][3]

// perspectiveMatrix用于求解透视，同时也为检测上部3x3矩阵是否奇异提供了简单方法。
perspectiveMatrix = matrix

for (i = 0; i < 3; i++)
    perspectiveMatrix[i][3] = 0

perspectiveMatrix[3][3] = 1

if (determinant(perspectiveMatrix) == 0)
    return false

// 首先，隔离透视。
if (matrix[0][3] != 0 || matrix[1][3] != 0 || matrix[2][3] != 0)
    // rightHandSide是方程的右侧。
    rightHandSide[0] = matrix[0][3]
    rightHandSide[1] = matrix[1][3]
    rightHandSide[2] = matrix[2][3]
    rightHandSide[3] = matrix[3][3]

    // 通过逆透视矩阵求解方程，并将rightHandSide乘以逆矩阵。
    inversePerspectiveMatrix = inverse(perspectiveMatrix)
    transposedInversePerspectiveMatrix = transposeMatrix4(inversePerspectiveMatrix)
    perspective = multVecMatrix(rightHandSide, transposedInversePerspectiveMatrix)
else
    // 无透视。
    perspective[0] = perspective[1] = perspective[2] = 0
    perspective[3] = 1

// 接下来处理平移
for (i = 0; i < 3; i++)
    translate[i] = matrix[3][i]

// 现在获取缩放和倾斜。“row”是一个包含3维向量的3元素数组
for (i = 0; i < 3; i++)
    row[i][0] = matrix[i][0]
    row[i][1] = matrix[i][1]
    row[i][2] = matrix[i][2]

// 计算X缩放因子并归一化第一行。
scale[0] = length(row[0])
row[0] = normalize(row[0])

// 计算XY倾斜因子并使第二行与第一行正交。
skew[0] = dot(row[0], row[1])
row[1] = combine(row[1], row[0], 1.0, -skew[0])

// 现在，计算Y缩放并归一化第二行。
scale[1] = length(row[1])
row[1] = normalize(row[1])
skew[0] /= scale[1];

// 计算XZ和YZ倾斜，使第三行正交
skew[1] = dot(row[0], row[2])
row[2] = combine(row[2], row[0], 1.0, -skew[1])
skew[2] = dot(row[1], row[2])
row[2] = combine(row[2], row[1], 1.0, -skew[2])

// 接下来，获取Z缩放并归一化第三行。
scale[2] = length(row[2])
row[2] = normalize(row[2])
skew[1] /= scale[2]
skew[2] /= scale[2]

// 此时，矩阵（在行中）是正交归一化的。
// 检查坐标系翻转。如果行列式为-1，则取反矩阵和缩放因子。
pdum3 = cross(row[1], row[2])
if (dot(row[0], pdum3) < 0)
    for (i = 0; i < 3; i++)
        scale[i] *= -1;
        row[i][0] *= -1
        row[i][1] *= -1
        row[i][2] *= -1

// 现在，提取旋转
quaternion[0] = 0.5 * sqrt(max(1 + row[0][0] - row[1][1] - row[2][2], 0))
quaternion[1] = 0.5 * sqrt(max(1 - row[0][0] + row[1][1] - row[2][2], 0))
quaternion[2] = 0.5 * sqrt(max(1 - row[0][0] - row[1][1] + row[2][2], 0))
quaternion[3] = 0.5 * sqrt(max(1 + row[0][0] + row[1][1] + row[2][2], 0))

if (row[2][1] > row[1][2])
    quaternion[0] = -quaternion[0]
if (row[0][2] > row[2][0])
    quaternion[1] = -quaternion[1]
if (row[1][0] > row[0][1])
    quaternion[2] = -quaternion[2]

return true

13.1.2. 分解后的三维矩阵值的插值

源矩阵的分解值中的每个组件（平移、缩放、倾斜和透视）都与目标矩阵中的对应组件线性插值。

注意: 例如，源矩阵的translate[0]与目标矩阵的translate[0]数值插值，结果用于设置动画元素的平移。

源矩阵的分解四元数与目标矩阵的分解四元数使用球面线性插值（Slerp）进行插值，伪代码如下所示：

输入:  quaternionA   ; 一个4维向量
        quaternionB   ; 一个4维向量
        t             ; 插值参数，0 <= t <= 1
输出: quaternionDst ; 一个4维向量


product = dot(quaternionA, quaternionB)

// 将product限制在-1.0 <= product <= 1.0
product = min(product, 1.0)
product = max(product, -1.0)

if (abs(product) == 1.0)
   quaternionDst = quaternionA
   return

theta = acos(product)
w = sin(t * theta) / sqrt(1 - product * product)

for (i = 0; i < 4; i++)
  quaternionA[i] *= cos(t * theta) - product * w
  quaternionB[i] *= w
  quaternionDst[i] = quaternionA[i] + quaternionB[i]

return

13.1.3. 重新组合为三维矩阵

插值后，结果值用于变换元素的用户空间。使用这些值的一种方式是将它们重新组合成一个4x4矩阵。可以按照以下伪代码进行操作：

输入:  translation ; 一个3维向量
        scale       ; 一个3维向量
        skew        ; XY、XZ、YZ倾斜因子表示为3维向量
        perspective ; 一个4维向量
        quaternion  ; 一个4维向量
输出: matrix      ; 一个4x4矩阵

支持函数（matrix是一个4x4矩阵）:
  matrix  multiply(matrix a, matrix b)   返回a * b的4x4矩阵乘积

// 应用透视
for (i = 0; i < 4; i++)
  matrix[i][3] = perspective[i]

// 应用平移
for (i = 0; i < 4; i++)
  for (j = 0; j < 3; j++)
    matrix[3][i] += translation[j] * matrix[j][i]

// 应用旋转
x = quaternion[0]
y = quaternion[1]
z = quaternion[2]
w = quaternion[3]

// 从四元数构造一个复合旋转矩阵
// rotationMatrix最初是一个单位4x4矩阵
rotationMatrix[0][0] = 1 - 2 * (y * y + z * z)
rotationMatrix[0][1] = 2 * (x * y - z * w)
rotationMatrix[0][2] = 2 * (x * z + y * w)
rotationMatrix[1][0] = 2 * (x * y + z * w)
rotationMatrix[1][1] = 1 - 2 * (x * x + z * z)
rotationMatrix[1][2] = 2 * (y * z - x * w)
rotationMatrix[2][0] = 2 * (x * z - y * w)
rotationMatrix[2][1] = 2 * (y * z + x * w)
rotationMatrix[2][2] = 1 - 2 * (x * x + y * y)

matrix = multiply(matrix, rotationMatrix)

// 应用倾斜
// temp最初是一个单位4x4矩阵
if (skew[2])
    temp[2][1] = skew[2]
    matrix = multiply(matrix, temp)

if (skew[1])
    temp[2][1] = 0
    temp[2][0] = skew[1]
    matrix = multiply(matrix, temp)

if (skew[0])
    temp[2][0] = 0
    temp[1][0] = skew[0]
    matrix = multiply(matrix, temp)

// 应用缩放
for (i = 0; i < 3; i++)
  for (j = 0; j < 4; j++)
    matrix[i][j] *= scale[i]

return

14. 原始和派生变换函数的插值

两个具有相同名称和相同参数数量的变换函数在不进行转换的情况下进行数值插值。计算后的值将保持为相同的变换函数类型，具有相同数量的参数。对于<matrix()>、<matrix3d()> 和<perspective()>适用特殊规则。

变换函数<matrix()>、matrix3d() 和 perspective() 首先转换为4x4矩阵，然后按照矩阵插值中定义的方式进行插值。

对于具有原始rotate3d()的插值，变换函数的方向向量首先进行归一化。如果归一化后的向量不相等且两个旋转角度均不为零，则变换函数首先转换为4x4矩阵，并按照矩阵插值中定义的方式进行插值。否则，旋转角度将以数值方式插值，并使用非零角度的旋转向量，或者如果两个角度都为零，则使用(0, 0, 1)。

两个变换函数translate(0) 和 translate(100px)属于相同类型，具有相同的参数数量，因此可以数值插值。translateX(100px)不属于相同类型，而translate(100px, 0)没有相同的参数数量，因此这些变换函数在没有进行转换步骤的情况下无法插值。

具有相同原始类型的不同类型变换函数或具有不同参数数量的相同类型变换函数可以插值。两个变换函数首先需要转换为共同的原始类型，然后再进行数值插值。计算后的值将是具有结果插值参数的原始类型。

以下示例描述了在悬停在div框上时从translateX(100px)到translateY(100px)的3秒过渡。这两个变换函数派生自相同的原始translate()，因此可以插值。

div {  
  transform: translateX(100px);  
}

div:hover {  
  transform: translateY(100px);  
  transition: transform 3s;
}

在过渡期间，两个变换函数都转换为共同的原始函数。translateX(100px)转换为translate(100px, 0)，translateY(100px)转换为translate(0, 100px)。然后这两个变换函数可以数值插值。

如果两个变换函数在二维空间中共享一个原始函数，则两个变换函数都会转换为二维原始函数。如果一个或两个变换函数是三维变换函数，则使用共同的三维原始函数。

在此示例中，二维变换函数被动画化为三维变换函数。共同的原始函数是translate3d()。

div {  
  transform: translateX(100px);  
}

div:hover {  
  transform: translateZ(100px);  
  transition: transform 3s;  
}

首先translateX(100px)转换为translate3d(100px, 0, 0)，而translateZ(100px)则转换为translate3d(0, 0, 100px)。然后这两个转换后的变换函数进行数值插值。

15. 变换列表的加法与累积

加法将两个变换列表 V_a 和 V_b定义为列表的连接，使得 V_result 等于 V_b 追加到 V_a。

累积两个变换列表V_a和 V_b遵循与插值相同的步骤，以匹配变换函数，包括用恒等变换函数填充列表，将none转换为恒等变换函数，并在必要时将两个参数转换为矩阵（请参阅CSS Transforms 1 § 11 变换的插值）。然而，个别参数不是通过插值，而是通过算术加法来组合——除了参数值为1的情况恒等变换函数（例如缩放参数和矩阵元素m11、m22、m33和m44），它们通过基于1的值的累积如下组合：

V_result = V_a + V_b - 1

上述定义保留了累积的初衷，即 V_b 作为 V_a的增量，并允许如下动画：

div.animate(
  { transform: ['scale(1)', 'scale(2)'] },
  {
    duration: 1000,
    easing: 'ease',
  }
);

在扩展如下时产生预期的行为：

div.animate(
  { transform: ['scale(1)', 'scale(2)'] },
  {
    duration: 1000,
    easing: 'ease',
    iterations: 5,
    iterationComposite: 'accumulate',
  }
);

15.1. 加法的中性元素

一些动画需要一个中性元素进行加法运算。对于变换函数来说，这个中性元素是标量或标量列表，值为0。变换函数的中性元素示例如下：translate(0)、translate3d(0, 0, 0)、translateX(0)、translateY(0)、translateZ(0)、scale(0)、scaleX(0)、 scaleY(0)、scaleZ(0)、rotate(0)、 rotate3d(vx, vy, vz, 0)（其中v是上下文相关的向量）、rotateX(0)、rotateY(0)、rotateZ(0)、 skew(0, 0)、skewX(0)、skewY(0)、 matrix(0, 0, 0, 0, 0, 0)、matrix3d(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)和perspective(none)。

注意: 当动画的目标或起点为加法的中性元素时，<matrix()>、matrix3d()和perspective() 会回退为离散动画（参见§ 13 矩阵的插值）。

16. 变换函数的数学描述

从数学上讲，所有的变换函数都可以表示为如下形式的4x4变换矩阵：

$$\begin{bmatrix} m11 & m21 & m31 & m41 \\ m12 & m22 & m32 & m42 \\ m13 & m23 & m33 & m43 \\ m14 & m24 & m34 & m44 \end{bmatrix}$$

矩阵中的一个平移单位等于元素本地坐标系中的1像素。

参数tx、ty和tz的3D平移等效于矩阵：
$$\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
参数sx、sy和sz的3D缩放等效于矩阵：
$$\begin{bmatrix} sx & 0 & 0 & 0 \\ 0 & sy & 0 & 0 \\ 0 & 0 & sz & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
向量[x,y,z]和参数alpha的3D旋转等效于矩阵：
$$\begin{bmatrix} 1 - 2 \cdot (y^2 + z^2) \cdot sq & 2 \cdot (x \cdot y \cdot sq - z \cdot sc) & 2 \cdot (x \cdot z \cdot sq + y \cdot sc) & 0 \\ 2 \cdot (x \cdot y \cdot sq + z \cdot sc) & 1 - 2 \cdot (x^2 + z^2) \cdot sq & 2 \cdot (y \cdot z \cdot sq - x \cdot sc) & 0 \\ 2 \cdot (x \cdot z \cdot sq - y \cdot sc) & 2 \cdot (y \cdot z \cdot sq + x \cdot sc) & 1 - 2 \cdot (x^2 + y^2) \cdot sq & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

其中：

$$sc = \sin (\alpha/2) \cdot \cos (\alpha/2)$$ $$sq = \sin^2 (\alpha/2)$$

其中x、y和z已被归一化（即给定的x、y和z值已除以它们平方和的平方根）。

请注意，这意味着围绕X轴的旋转简化为：
$$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 - 2 \cdot sq & -2 \cdot sc & 0 \\ 0 & 2 \cdot sc & 1 - 2 \cdot sq & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

围绕Y轴的旋转简化为：

$$\begin{bmatrix} 1 - 2 \cdot sq & 0 & 2 \cdot sc & 0 \\ 0 & 1 & 0 & 0 \\ -2 \cdot sc & 0 & 1 - 2 \cdot sq & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

围绕Z轴的旋转简化为：

$$\begin{bmatrix} 1 - 2 \cdot sq & -2 \cdot sc & 0 & 0 \\ 2 \cdot sc & 1 - 2 \cdot sq & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
参数d的透视投影矩阵等效于矩阵：
$$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & -1/d & 1 \end{bmatrix}$$

如果参数d为none，它被视为无穷大（结果矩阵为单位矩阵）。

17. SVG 变换属性

本规范还将引入新的展示属性变换原点, 透视, 透视原点, 变换样式和背面可见性。

新引入的展示属性值按照 SVG 数据类型的语法规则进行解析，详见 [SVG11]。

18. SVG 动画

18.1. `animate` 和 `set` 元素

引入的展示属性透视, 透视原点, 变换样式和背面可见性是可动画的。变换样式和背面可见性不具有累加性。

19. 更多问题

根据 https://lists.w3.org/Archives/Public/www-style/2015Mar/0371.html，工作组决定添加一个公式，用于将变换分解为统一的“缩放” （规范已经定义了如何将其分解为scaleX/Y/Z），供SVG的非缩放描边规范等使用。公式在此定义。

20. 安全和隐私注意事项

本规范未引入任何新的安全或隐私注意事项。

CSS 变换模块 第 2 级

W3C 工作草案, 2021年11月9日

摘要

文档状态